Исследование скорости травления различных пленок в установке плазменной обработки МРС
Процесс травления материала является неотъемлемой частью производства полупроводниковых приборов. Существует «сухой» способ травления с помощью установок ионно-плазменной обработки низкого давления [1]. Благодаря плазменной обработке происходит травление материала без вредного влияния на экологию по сравнению с жидкостным методом травления [2].
Для проведения травления на определенную толщину необходимо знать скорость травления, которая зависит от обрабатываемого материала, газовой среды, давления, мощности плазмы, а также от времени [3].
В данной статье исследована скорость ионно-плазменного травления пленок оксида алюминия Al2O3 и меди Cu, нанесенных на кварцевые резонаторы. Контроль толщины осуществлялся на основе метода измерения толщины пленки кварцевыми резонаторами [4].
Изменение толщины после процессов напыления и травления измерялось при помощи кварцевых резонаторов. Зная номинальную резонансную частоту кварца и изменение частоты после обработки, можно рассчитать изменение удельной массы на поверхности электродов. Если после обработки частота кварцевого резонатора увеличивается, то удельная масса материала на поверхности электродов уменьшается; если же частота уменьшается, то удельная масса увеличивается. Изменение массы показывает, насколько изменилась толщина пленки. С помощью уравнения Зауэрбри, преобразовывающего частоту кварцевого резонатора в массу, были найдены изменения удельной массы после нанесения пленки и после травления [5]. Поскольку скорость травления определяется как толщина стравливаемого материала в единицу времени, то удельная масса была переведена в толщину пленки, с использованием времени обработки и плотности материала.
По проведенным экспериментам построены графики зависимости скорости травления от времени V(t) и толщины пленки от времени h(t), а также относительного изменения частоты кварцевых резонаторов от времени δ(t), показанные на рис. 1, 2 соответственно.
Данные эксперимента показали, что с течением времени скорость травления пленки меди уменьшается, причем при проведении повторной обработки того же кварцевого резонатора при неизменном режиме обработки травления пленки не происходит. Максимальная скорость травления 2,72 нм/мин. Травление пленки Al2O3 происходит лишь на временном промежутке 1–1,5 мин и более 2 мин. На промежутке 1,5–2 мин масса кварцевого резонатора увеличивается, что связано с процессом окисления Al.
Зависимость относительного изменения частоты от времени δ(t) похожа на зависимость толщины от времени h(t). Минимальные изменения произошли для меди при 1,5 мин. В случае с Al2O3 график δ(t) имеет отрицательные значения, что также говорит о том, что процесс травления на этом промежутке не происходит.
- Высоцкий Б. Ф. Конструирование аппаратуры на БИС и СБИС. М.: Радио и связь, 1989.
- Павленко А. Д., Рогожин А. А., Васильев Д. Д. Влияние физических и геометрических параметров установки плазменной обработки на угол смачиваемости стеклянной подложки. 11‑я Всероссийская конференция молодых ученых и специалистов «Будущее машиностроения России» МГТУ им. Н. Э. Баумана, МТ‑11, 24–27 сентября
- Wayne M. Moreau. Semiconductor Lithography: Principles, Practices, and Materials. SRI lnternational Menlo Park, California, 1988.
- Sauerbrey G. Verwendung von Schwingquarzen zur Wagung dunner Schichten und zur Mikrowagung. Physikalischen Institut der Technischen Universitat Berlin, 1959.
- Wang X., Li M., Long S. C. Memory from Sauerbrey Equation: A Case in Coated Quartz Crystal Microbalance in terms of Ammonia. Hindawi Publishing Corporation Mathematical Problems in Engineering, 2011.

 отправка...
отправка...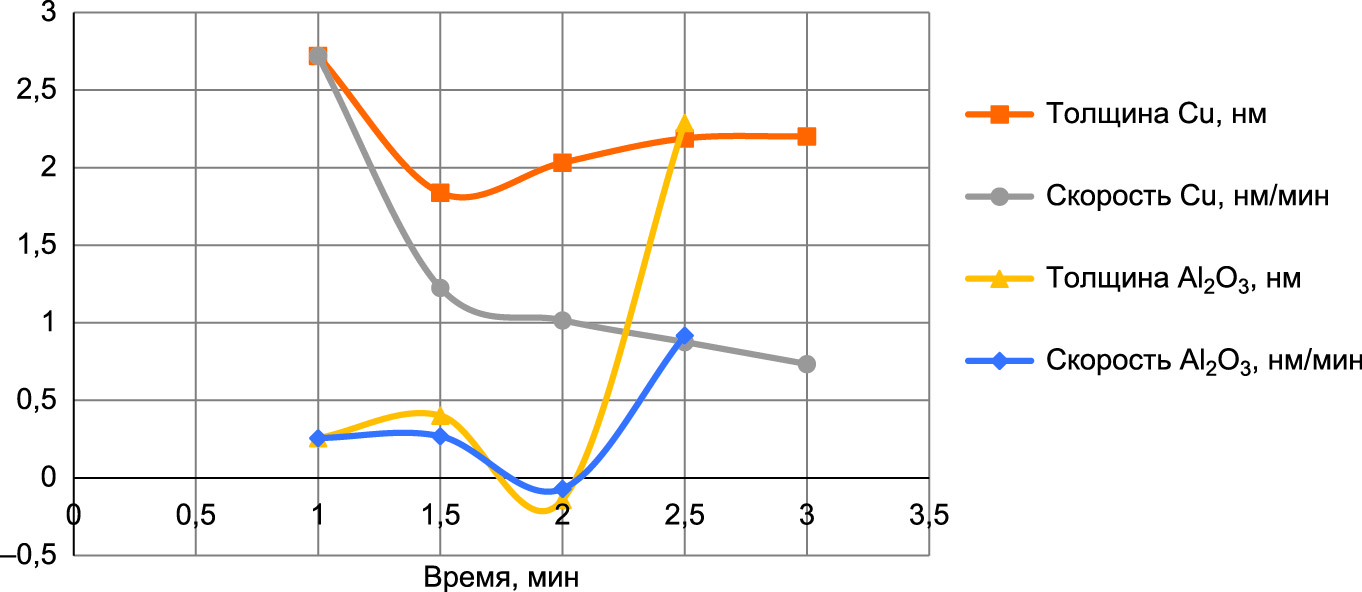

 17 августа, 2021
17 августа, 2021